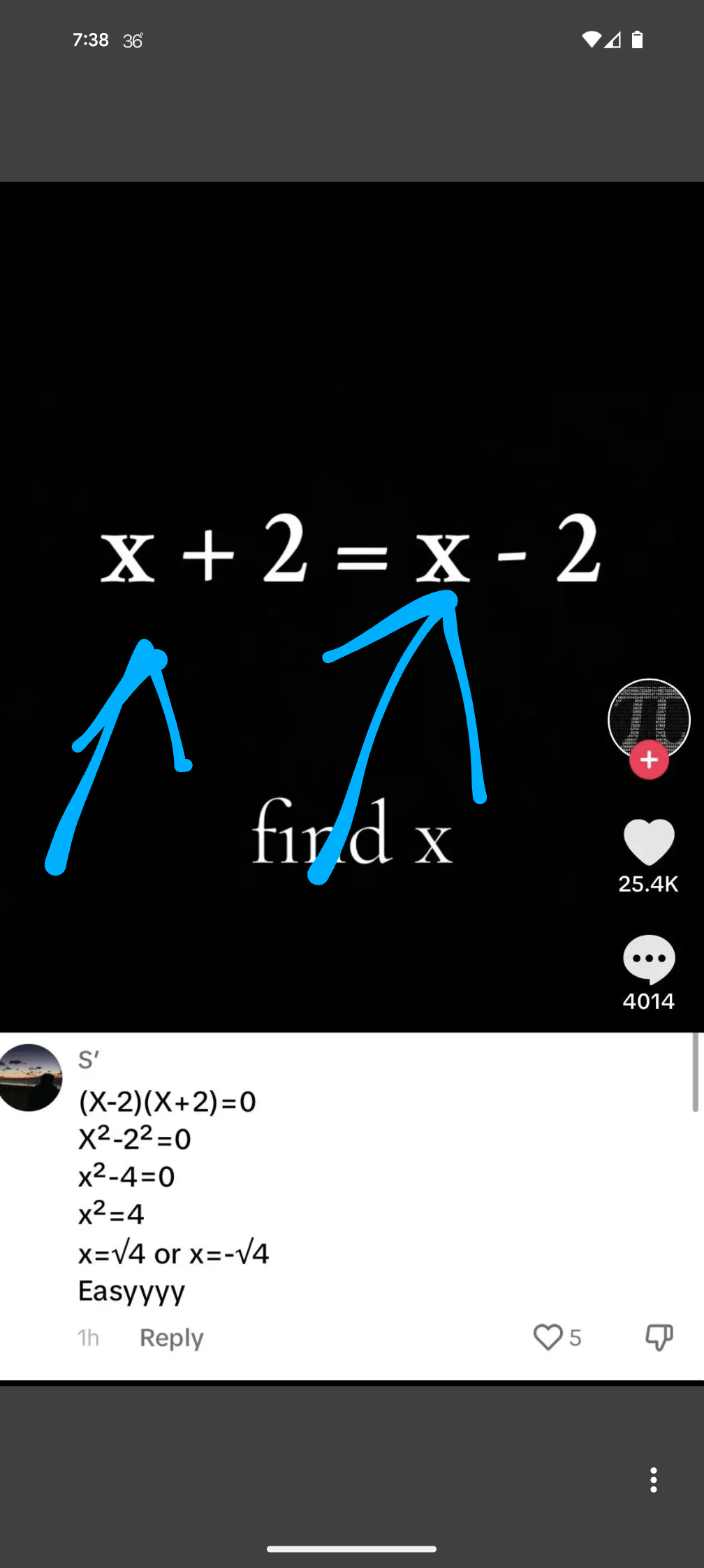
x + 2 = x - 2
I found x, twice even. EZ
That is probably the most correct answer.
deleted by creator
Probably more correct than that.
I find this meme and this comment section distressing. Y’all are bad at basic algebra.
Carry on, I guess.
Do enlighten us.
Subtract
xfrom both sides of the equation. You get2 = -2which is incorrect and nonsensical.I know that, but @[email protected] said that most of us here are bad at basic algebra. Not that I’m great at it (I had an 8 average in all 4 maths in uni), but I do believe that most of us here were correct. This is unsolvable using classic algebra.
Just to be clear: the comment was meant in a lighthearted way and not meant to be taken personally, especially toward those who are confident with their math skills.
My bad.
Apology accepted 😊.
To be honest, my comment was meant to have double meaning. On one hand, I was certain that this thing can’t be solved with classic algebra. On the other, it’s been a while since I’ve done any math with pen and paper, so I figured “I might have forgotten something that could make this solvable”. In either case, I was curious 😂.
2 = -2, easy
Can someone smart explain it to dumb me
Explanation: How did they get from
x + 2 = x - 2
to
(x+2)(x-2)=0?
That’s not a valid step.
To further clarify,
(x+2)(x-2) means to take the result of X+2 and times it with the result of x-2.
While it is common in algebra to bring the other side over, in order to simplify it, this isn’t how you’d do it.
Here, you’d either cancel out the X (by removing it on both sides) or the -2 (by adding 2 to both sides) over to make 2=-2 or X+4=X respectively, which are both nonsense equations.
and times it with the result
and multiply it with the result
Both are correct.
Not really, no… “times” is not a verb. You can multiply 2 by 2, and you can express that as “2 times 2”, but it is not correct to “times 2 by 2”.
…seems to be pretty correct to me:
https://www.wordreference.com/es/translation.asp?tranword=multiplying
Not sure what you think the relevance of a Spanish-English translation of the word “multiplying” has here… but nonetheless, you can see the correct usage of the word “multiply” versus the word “times” in my explanation above. For further clarification I would suggest a real dictionary, like Oxford, Meriam-Webster, etc.
I’m sure plenty of people will continue to make the mistake and it will become an accepted variant, though I wouldn’t consider it to be the correct usage of the word. Similar to the word “irregardless”, it’s a word, it’s used incorrectly in place of “regardless” very often, and therefore is an accepted variant. It’s just not the correct word to use. This is why I offered you my initial correction.
they start off with S’ though… looks like they pretended to try to derive?
I thought that was their profile name
oh fuck me, you seem to be correct
Almost everything is wrong in his answer.
The correct answer is, it’s unsolvable.
X + 2 = X - 2
X - X = - 2 - 2
0 = - 4
The real correct answer is that it only works mod 4
Only the first step is wrong.
Yeah, my bad 👍.
deleted by creator
It’s not solvable using traditional algebra.
Typically you would try to get all of the variables on one side, and all of the numbers on the other.
So in this instance, you’d start by moving them around to get things together:
x+2 = x-2
x+2-x = -2
x-x = -2-2But then you simplify, and cancel out any variables that need to be cancelled. In this case we see “x-x” so that cancels out to 0. And we see -2-2 which simplifies into -4. So the end result is:
0=-4
Which is obviously a nonsense answer. In the original post, homeslice did the first step wrong, moved everything over to the left incorrectly, (inadvertently setting the whole equation equal to 0) and the whole thing was downhill from there; Since the first step of their solution was wrong, everything behind it was also wrong.
You know how you sometimes make a mistake in one line, but after doing a few lines, you go back to actually writing the equation correctly? Happened to me all the time in uni. It’s basically because you were thinking of doing the next line or whatever, and you just forgot that a var or const was somewhere in there, or you just didn’t copy (or copy it correctly) in the next line, but the memory of that var/const remained in your brain, so after doing a few lines, the equation is now simple enough so your brain knows something should be there, but it’s missing. Sure, we almost always caught up with the mistake, go back, correct the last few lines and carry on. But, every once in a while, you don’t, and you carry on solving the equation, and you get a correct solution, but from a purely mathematical standpoint, yes, that solution is not correct.
My math proffesor in uni had an interesting take on this. He said, you didn’t do 1 mistake and then correct it to get the right answer, but you actually made 2… which is worse… according to him. And I have to say, at that time, I didn’t agree, but let’s be honest… he is correct. So, he went a lot harder on those students that did this type of mistake than the ones that just made 1 and carried on solving the equation like nothing happened.
nah… its still just one error: that of transcribing your process.
it’s like a cosmic ray randomly changed a digit in the memory cells that hold the stringbuffer prepared to be printed.
and then the computation carries on with the internal representation of the whole process still with correct data.
i understand your profs pov though
From an engineering standpoint, I don’t agree with him. We make errors all the time, it’s basically how we learn how to do things the right way (try, fail, repeat). Not to mention rounding errors, we also make GIGANTIC ones (not all the time, but still).
But, he’s a mathematician, not an engineer. So, as I said, from a purely mathematical standpoint, yes, he is correct.
well, yeah… xD as i said, i understand that pov. if that printout WAS the process, then yes.
and for an alien that only receives that printout milled into a goldbar attached to a satellite: that would be a bummer ;3
There isn’t a valid answer to the question.
Ignore the numbers, and just think about this:
Is there a number that you can add 2 to, that would equal the same about as if you subtracted 2 from it?
The answer is no.So the person, who is pretending to be smart, just did a bunch of fake math.
Also √4 = 2, so the “answer” they have is just them trying to re-write the question x + 2 = x - 2.√4=±2
The square root of x is usually defined as the positive real number that squares to x, so x^2 = 4 => x = ±2 but sqrt(4) = 2, not ±2
The complex sqrt function is multivalued, but that opens a whole other can of worms
And even if you allowed sqrt(4) = ±2, it would still be invalid to evaluate it to -2 on one side of the equation, but then use +2 on the other side.
Of course, you can only choose one at a time, not mix and match, lol 😂.
Oh yeah, you’re right, now I remembered 🤦. Been a while 😂, almost 20 years.
Right there:
I know we’re supposed to assume x is a real number, but this could be true if x is a sinusoidal waveform with period = 4. The question didn’t specify the range or what set of numbers on which x is defined.
You mean irrational and real axis?
Would it be a rabbit hole to try and find any merit in this solution when interpreting it as: “if x is in a superposition of 2 and -2, the
x + 2 = x - 2would be true in 1/4 of the observations”, or something like that?It is the closest thing to a “solution” that I can imagine, but doesn’t fit any laws that I know of or understand, and would probably break down on any scrutiny, but it feels like something is there.
x cant be both values at the same time, not under what most people consider to be math. Feel free to write your own logical system and see where that takes you, though.
I think the only “solution” that works is addition/subtraction under mod 4 (or mod 2 I suppose) like another poster suggested. Then we’d have:
X + 2 = x - 2
X + 4 = x (Add 2 to both sides)
X + 0 = x (4 = 0 mod 4)
X = x (True for all x)
(True for all x)
But not true for any rational number if you try it in the equation.
Thus, this is not a solution. The equation is unsolvable with rational numbers.
Correct, not solvable with rational numbers. I should have been more clear. When we’re doing arithmetic modulo x, it’s assumed to be with integers.
To be clear, this is a solution only in Z_4 which is not what most people mean when they’re look for answers to algebra problems. And it would be a solution for all x in Z_4 (which are integers, see this page that I assume is a good summary)
Yes, that is correct, this is solvable in modular algebra… but, in that case, the tripple horizontal line equal sign should have been used, not the double horizontal line one, which of course indicates classic algebra.
Also true but I’m not sure how to do that on my phone so I gave up
Maybe lemmy can do mathjax someday
I was talking about the person that posted the equation. They should have found a way if they wanted this thing solved, lol 😂.
Don’t overthink it, it’s made to be unsolvable on purpose, just to test how much math your average Joe knows.
Haha I got that :) @[email protected] is right, I was halfheartedly looking for a logic system in which it could make sense. Still, I would have major issues with the first step as it is shown, but I am wondering about systems where, say, each
x <- {..}, then what would be the set, and the probability of the correct solution.Something I need to be more awake for, and it may be easier to solve without resorting to powers and roots, haha.
Reply to self: really not that useful. That would be the same as just throwing all variables/coordinates of the solution in a set, forgetting their names and then filling them back in as some kind of madlibs experiment. And multiple solutions don’t grow with the exponent on x, that is just an odd/even thing. Don’t know shat I was thinking…
I can tell you one thing, the equation makes perfect sense if x --> inf.
Clearly X= |2> + |-2> 😅
⬆️ this poster didn’t normalize their linear combination of wave functions
x=4/0






